Introducción
El viento llega a
la turbina eólica con una cierta energía cinética y cederá parte de la misma a
los álabes de la turbina para hacerla girar, por lo que al salir de ella lo hace
con una menor energía cinética.
Cuanto mayor es la
energía cinética extraída del viento por el aerogenerador, mayor será el
frenado que sufre el viento que deja al aerogenerador por el lado izquierdo del
dibujo. Si teóricamente fuese posible extraer toda la energía del viento, el
aire saldría con velocidad nula, o sea que el aire no podría abandonar la
turbina. En este caso no sería posible extraer ninguna energía, ya que tampoco
entraría aire en el rotor del aerogenerador. El otro caso extremo, sería que el
viento pasara por el tubo de viento sin ningún impedimento: tampoco será posible extraer energía del viento.
Entre estos dos
extremos existe un valor para el cual es más eficiente la conversión de la
energía del viento en energía mecánica. Este valor se obtiene de la formulación
de 1919, realizada por el físico alemán Albert Betz, y conocida como Ley de
Betz.
Tesis de la
Ley de Betz
Para obtener con
un aerogenerador la máxima potencia del viento se deberá frenar al mismo en 1/3
de su velocidad y la máxima potencia es 0,59 veces la potencia que entrega el
viento.
Demostración de la Ley de Betz
El viento llega a la turbina con una cierta
energía cinética:
Ec1 = ½ . m . v12 (1)
y entregará parte de esa energía a los álabes de la turbina
haciéndola girar, por lo que sale de la turbina con la energía cinética
siguiente :
Ec2 = ½ . m . v22 (1´)
La energía cinética entregada a la turbina por el viento,
vendrá dada por la diferencia entre la energía cinética que tiene la masa de
aire(viento) cuando entra, menos la que tiene cuando sale de la turbina, o sea
:
Ect = ½ . m . v12 - ½ . m
. v22 =
½ . m . (v12 - v22 ) (2)
El caudal de aire que incide sobre los álabes de la
turbina será:
Q = v . S (3)
Donde Q es el caudal de aire en m3/seg,, v es la velocidad del viento sobre los álabes
y S el área barrida por ellos.
Si ahora multiplicamos ambos miembros de la expresión (3)
por la densidad del aire d, tenemos :
d . Q = d . v . S
= m´ (4)
Donde m´
es la masa de aire(viento)que incide sobre el rotor por segundo.
Si ahora
reemplazamos en la expresión (2) la masa m por la masa m´ que incide sobre el rotor
por segundo, tendremos energía por unidad de tiempo, que no es otra cosa que la
potencia de esa turbina de viento :
P = ½ .
m´ . (v12 -
v22 ) (5)
Si ahora aceptamos que la velocidad del viento en los
álabes es igual al promedio de las velocidades del viento antes y después de
entrar en la turbina :
v = (v1+v2)/2 (6)
Si ahora reemplazamos la expresión (6) en la (4), tenemos :
m´ = d . (v1+v2)/2
. S (7)
Reemplazando la (7) en la (5), tendremos la siguiente
expresión para la potencia extraída del viento:
___________________________
P = (d/4) . (v12 - v22) (v1+v2) .
S (8) *
___________________________
*Obsérvese que si v1
= v2, la
potencia extraída del viento sería cero, lo cual es correcto.
La potencia total de una corriente de
viento no perturbada a través de exactamente la misma área S, sin ningún rotor
que bloquee el viento, será: (llamando a esta potencia P0)
P0 = (d/2)
. v13 . S
(9) **
** Obsérvese que esta expresión no se obtiene haciendo
iguales las velocidades de entrada y salida en (8), porque no es un caso
particular de ella, sino otro caso fisico. La (8) es la potencia que
extrae la turbina del viento y la (9) es la potencia del viento sin
perturbar, o sea la potencia total del viento. Esta expresión
se obtiene de la siguiente manera:
Ec = ½ . m . v12
d . Q = d . v . S = m
Ec = ½ . dvS . v12 = P0 = (d/2) . v13 . S
Dividiendo (8) y (9) miembro a miembro entre si, obtenemos :
____________________________________
P /
P0 = (1/2) . {1 - (v2 / v1)2) (1 + (v2 / v1)} (10)
____________________________________
La expresión (10)
nos indica cuantas veces la potencia total del viento puede ser extraída para
mover los álabes de la turbina.
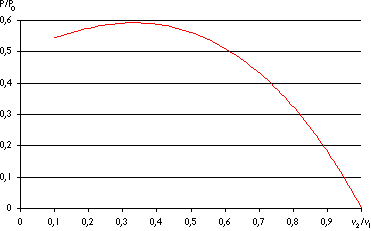
Podemos dibujar P /P0 en función de v2/v1:
Podemos ver que la función alcanza su máximo para v2/v1 = 1/3= 0,333…, y que el valor
máximo de la potencia extraída del viento es de 0,59 veces ó 16/27 la
potencia total del viento.

muy bueno el artículo Jorge!
ResponderEliminarun abrazo
mario c damonte